Kapitel 2 Zugänge zu Zufall und Wahrscheinlichkeit

Bevor ein möglicher Weg zu den Konfidenzintervallen aufgezeigt wird, wird der Fokus noch auf Zufall und Wahrscheinlichkeit gelegt, da grundsätzliche Vorstellungen in diesem Bereich vonnöten sind, um sich mit der Materie näher zu beschäftigen. Laut Freudentahl ist es auch keine neue Idee “to uncover the experimental roots of the probability concept” (Freudenthal 1972, 484).

2.1 Grundvorstellungen

GrundvorstellungenGrundvorstellungen sind tragfähige mentale Modelle für einen Begriff oder ein Verfahren. Mit diesen Grundvorstellungen schafft man sich eine anschauliche Repräsentation von abstrakten Begriffen. Weiters ist es dadurch möglich außer- und innermathematische Zusammenhänge herzustellen. Generell sind Grundvorstellungen dynamisch und unterliegen somit einer ständigen Veränderung. Im schulischen Kontext spricht man von zwei verschiedenen Arten von Grundvorstellungen. Die primären Grundvorstellungen, welche ihre Wurzeln in Handlungen haben, und die sekundären Grundvorstellungen, welche durch fachliche Unterweisungen entstehen (Schmelzer 2018, 1611). Grundvorstellungen sind einerseits die Basis für das Erlernen von stochastischen Methoden und Konzepten und andererseits auch die Voraussetzung, dass man mathematische Situationen außerhalb des Mathematikunterrichts wieder erkennt und richtig interpretieren kann (Schmelzer 2018, 1613).

[Gründe für Grundvorstellungen]Die erste Frage, welche sich hier stellt, ist: Wozu werden Grundvorstellungen zum Zufall benötigt? Innermathematisch ist diese Frage einfach beantwortet, denn die Stochastik ist ein essentielles Teilgebiet der Mathematik. Somit kann man die Stochastik auch nicht aus einer mathematischen Grundausbildung ausschließen. Jedoch hat Stochastik auch außermathematisch eine Daseinsberechtigung. Gerade Statistik, aber auch Wahrscheinlichkeitsrechnungen spielen in vielen Fachgebieten eine große oder gar zentrale Rolle. Dabei ist wichtig, dass der stochastische Charakter einer Situation erkannt wird. Erst dann kann eine Verbindung zwischen den gelernten stochastischen Ideen und Inhalten und der Situation gelingen. Dafür werden angemessene Grundvorstellungen benötigt. Auch im Unterricht sind gut entwickelte Grundvorstellungen essenziell. Denn somit legt man den Grundstein für weitere stochastische Inhalte (Hauer-Typpelt 2010, 1). Diese Grundvorstellungen sind Teil einer umfassenden stochastischen Grundbildung. Gerade mit den neuen gesellschaftlichen oder auch wirtschaftlichen Hintergründen (Analyse und Interpretation von big data) müssen die SchülerInnen in der Lage sein, Daten und Wahrscheinlichkeiten verstehen, interpretieren und beurteilen zu können. Außerdem sollen sie basierend darauf auch eigenständige Argumentationen entwickeln (Schnell und Eichler 2018, 115).

[Zufall]Für den Begriff Zufall benötigt man eine Grundvorstellung, da es sich hier um einen Begriff handelt, der nicht den “klassischen” Definition im Mathematikunterricht folgt. Da es keine exakte Begriffsdefinition für Zufall gibt, sollte man – auch und vor allem im Schulunterricht – einen anderen Zugang finden (Hauer-Typpelt 2010, 3). Insgesamt gibt es laut (Eichler und Vogel 2009) zwei Extrempositionen zum Begriff Zufall: Eine Position gibt an, dass alles Zufall sei. Die andere Position basiert darauf, dass es keinen Zufall gibt und alles, was als zufällig angesehen wird, ein Ausdruck für Unwissen sei. Eine Vorstellung zum Begriff Zufall kann durch Konfrontation und Bearbeitung verschiedener Settings, in welchen der Begriff Zufall eine Rolle spielt, aufgebaut werden (Hauer-Typpelt 2010, 3). Somit wäre das Aufbauen von Vorstellungen zum Begriff Zufall ähnlich dem Erlernen der Zahlen. Durch Abstraktion werden die Zahl und die verschiedenen Gegenstandsmengen getrennt. So haben beispielsweise drei Kreiden, drei Steine und drei Stühle die Zahl drei gemeinsam (Bruder u. a. 2015, 77). Dadurch wird auch deutlich, dass es hilfreich ist, mehrere verschiedene Kontexte und Situation zur Betrachtung einzubringen. Diese müssen nicht ausschließlich realweltliche Situationen, sondern können auch künstliche stochastische Situationen, wie eigene Aktivitäten mit Zufallsexperimenten, sein (Hauer-Typpelt 2010, 3).

[zufällige Zahlenfolgen]Wie man auch den Zufall nicht einfach definieren kann, so gestaltet es sich auch schwierig zu definieren, wann eine Zahlenfolge als “zufällig” gelten kann. Der Versuch von Richard Edler von Mises die Zufälligkeit einer Zahlenfolge als “fehlende Vorhersagbarkeit” zu definieren, war nicht erfolgreich. Sein Ansatz war: Eine Sequenz, welche nur aus den Ziffern 0 und 1 besteht, heißt dann zufällig, wenn es keine Regel gibt das nächste Glied – mit einer Wahrscheinlichkeit von 50 % – aus den vorherigen Gliedern abzuleiten. Das Problem bei diesem Ansatz war, dass von Mises nicht mathematisch präzisieren konnte, was man unter dieser Regel verstehen soll. Erfolgreiche Ansätze lieferten Kolmogorov und Gregory Chaitin zeitgleich in den 60er Jahren. Sie betiteln eine Zahlenfolgen als zufällig, wenn sie sich nicht durch eine kurze Zeichensequenz beschreiben lässt. Beispielsweise kann die Zahlenfolge 111…1 mit dem Befehl “schreibe lauter Einsen” oder die Zahlenfolge 0101…01 mit dem Befehl “wiederhole 01” abgekürzt werden. Jedoch bleibt bei diesem Ansatz noch unklar, wie man zeigen soll, dass es eine kürzere Beschreibung geben kann (Büchter und Henn 2005, 293).

[Wahrscheinlichkeit]Ohne einen angemessenen Wahrscheinlichkeitsbegriff kann man nicht fundiert über das Konzept “Zufall” sprechen. Aus diesem Grund gehört der Wahrscheinlichkeitsbegriff auch zu den Grundbegriffen der Stochastik. Oftmals wird nur die Laplace-Wahrscheinlichkeit mit dem Wahrscheinlichkeitsbegriff verknüpft. Jedoch ist auf Basis des Lehrplans dieser Wahrscheinlichkeitsbegriff zu wenig (Hauer-Typpelt 2010, 5). Büchter und Henn (2005) sprechen davon, dass Wahrscheinlichkeit immer etwas mit Ungewissheit zu tun hat. Weiters sollen damit einerseits Prognosen über den Ausgang eines zukünftigen Ereignisses oder andererseits eine Beurteilung über eingetretene Ereignisse abgegeben werden. Um einen Zugang zum Begriff “Wahrscheinlichkeit” zu bieten, kann wiederum mit verschiedenen Situationen (Experimenten) gearbeitet werden. Diese Experimente sollen nicht nur den Laplace’schen Wahrscheinlichkeitsbegriff im Fokus haben, sondern können auch den frequentistischen Wahrscheinlichkeitsbegriff (vgl. 2.2.1 empirischer Zugang) betreffen (Hauer-Typpelt 2010, 5).

[Primär- und Sekundärintuitionen]Für das Ausbilden von Grundvorstellungen muss besonders im Stochastikunterricht viel Zeit investiert werden, da sich in der Stochastik gerade die grundlegenden Begriffe “Zufall” und “Wahrscheinlichkeit” nicht definieren lassen und man somit eine adäquate Vorstellung benötigt. In der Anfangsphase spielen Primärintuitionen eine große Rolle (Hauer-Typpelt 2010, 12). Fischbein unterscheidet zwei Arten von Intuitionen: Die eben angesprochene “Primärintuition”, welche sich direkt aus den eigenen Erfahrungen ergibt, und die “Sekundärintuitionen”, welche durch die Behandlung von bestimmten Themen im Unterricht entwickelt werden. Dies zeigt auf, dass die Auseinandersetzung mit den bereits bestehenden Primärintuitionen, deren Weiterführung oder Berichtigung ein essentieller Teil des Stochastikunterrichts sind (Schnell 2014, 14:32). Im Text von Fischbein (2002) ist noch folgende Aussage zu den Sekundärintuitionen zu finden: “[W]e assume that under a systematic, instructional influence new intuitions, new cognitive beliefs may be created.”

2.2 Zugänge

Um adäquate Grundvorstellungen auszubilden, können verschiedene Situationen zur Betrachtung herangezogen werden. Im Stochastikunterricht sollten die verschiedenen Sichtweisen (empirische Sichtweise, theoretische Sichtweise und subjektive Sicht) einfließen (Hauer-Typpelt 2010, 5).

2.2.1 Empirischer Zugang

[frequentistische Interpretation]Der empirische Zugang oder die empirische Sichtweise ist stark mit der frequentistischen Wahrscheinlichkeit verknüpft. Dieser Zugang wird meist verwendet, wenn sich die Wahrscheinlichkeiten vorher nicht – theoretisch begründet – angeben lassen. Die frequentistische Wahrscheinlichkeit ist eine Schätzung der objektiven Wahrscheinlichkeit (Eichler und Vogel 2009, 169). Diese Wahrscheinlichkeiten besitzen einen hypothetischen Charakter, da diese durch die relativen Häufigkeiten eines Ereignisses eines Zufallsexperiments bei häufiger Durchführung abgeschätzt werden (Schnell 2014, 14:24). Mit zunehmender Versuchsanzahl verbessert sich die Genauigkeit der empirisch basierten Schätzung (Riemer 1991, 26).

[Empirie]Die freuqentistische Wahrscheinlichkeit wird erst, nachdem der zufällige Vorgang stattgefunden hat, ermittelt. Somit entspricht die frequentistische Wahrscheinlichkeit den relativen Häufigkeiten. Die Berechtigung dieses Ansatzes liefert das empirische Gesetz der großen Zahlen, welches salopp formuliert, die relativen Häufigkeiten bei sehr häufiger Durchführung eines Zufallsexperiments der tatsächlichen Wahrscheinlichkeit annähert (Eichler und Vogel 2009, 169). Laut Schmelzer (2018), S. 1613 beschreibt der frequentistische Wahrscheinlichkeitsbegriff die Wahrscheinlichkeit als Grenzwert der relativen Häufigkeiten in unendlich langen Versuchsserien. Jedoch ergeben sich für diese Aussage einige Probleme.

[empirisches Gesetz der großen Zahlen]Eine Stabilisierung der relativen Häufigkeiten bei häufiger Durchführung eines wiederholbaren Zufallsexperiments kann man zwar beobachten, jedoch lässt sich diese Stabilisierung nicht im mathematischen Sinn beweisen. Deshalb spricht man hier von einer Erfahrungstatsache, welche die Natur beschreibt und sich bewährt hat, aber eben nicht beweisbar ist. Aus diesem Grund spricht man auch von einem empirischen Gesetz (Büchter und Henn 2005, 145).

Das empirische Gesetz der großen Zahlen

Mit wachsender Versuchszahl stabilisiert sich die relative Häufigkeit eines beobachtbaren Ereignisses.

Jedoch kann das empirische Gesetz der großen Zahlen als ein gutes Modell herangezogen werden (Prömmel 2013, 63).

[Beweisversuch]Wenn man das empirische Gesetz der großen Zahlen näher betrachtet, kann man auf den Gedanken kommen, den Limes der relativen Häufigkeiten bei unendlich häufiger Durchführung zu verwenden. Diese Idee hat Richard Edler von Mises 1919 verfolgt. Seine Idee war es, den Begriff “Wahrscheinlichkeit” im Sinne der analytischen Definition eines Grenzwerts zu definieren. Diese Überlegung führte jedoch nicht zum Erfolg. Nehmen wir ein Ereignis \(E\) an, für welches eine reelle Zahl \(\mathbb{P}(E)\) existieren soll, mit \[\begin{align*} \mathbb{P}(E) = \lim_{n \rightarrow \infty} h_n(E). \end{align*}\] Wobei \(h_n\) die relativen Häufigkeiten des Ereignisses bei einer Versuchsanzahl von \(n\) ist. Wenn dieser Grenzwert existiert, dann müsste gelten, dass für jede positive Zahl \(\epsilon\) eine natürliche Zahl \(n_{\epsilon}\) exisitiert, sodass \[\begin{align*} |\mathbb{P}(E)-h_n(E)| < \epsilon \text{ für alle } m \leq m_{\epsilon} \end{align*}\]

gilt. Das kann jedoch nicht garantiert werden. Zwar wird nach Wahl eines \(\epsilon > 0\) die relative Häufigkeit ziemlich sicher nach einer bestimmten Zeit in den “\(\epsilon\)-Schlauch” \(\mathbb{P}(E) \pm \epsilon\) hineinlaufen, jedoch kann dieser Schlauch auch wieder verlassen werden (vgl. 2.1). Das bedeutet, dass es sich hier nicht um einen Grenzwert im analytischen Sinn handelt. Somit ist die Beweisidee von von Mises nicht korrekt und es kann kein geeignetes \(m_{\epsilon}\) gefunden werden (Büchter und Henn 2005, 145; Eichler und Vogel 2009, 88).

Figure 2.1: Die relativen Häufigkeiten müssen nicht im Epsilon-Schlauch bleiben.

Laut Büchter und Henn (2005) kann das empirische Gesetz nicht zur Definition der Wahrscheinlichkeit herangezogen werden, jedoch vermittelt es eine Grundvorstellung, denn das empirische Gesetz der großen Zahlen ist die Basis um mathematischen Wahrscheinlichkeitsaussagen Sinn zu verleihen (Schnell 2014, 14:18).

[Bernoulli’sches Gesetz der großen Zahlen]Durch das Bernoulli’sche Gesetz der großen Zahlen erklärt sich der Zusammenhang zwischen der relativen Häufigkeit und der Wahrscheinlichkeit (Schnell 2014, 14:22). Das Bernoulli’sche Gesetz gibt an, wie wahrscheinlich es ist, dass die relativen Häufigkeiten in einem vorgegebenen \(\epsilon\)-Schlauch bleiben. Dennoch garantiert auch dieses Gesetz nicht, dass die relativen Häufigkeiten im \(\epsilon\)-Schlauch bleiben. Denn das Gesetz gibt nur an, dass Abweichungen um mehr als \(\epsilon\) unwahrscheinlicher werden, wenn die Versuchsanzahl \(n\) des Zufallsexperiments wächst (Büchter und Henn 2005, 153). Dieses Gesetz ist auch mit dem Namen Schwaches Gesetz der großen Zahlen bekannt und lautet wie folgt:

Schwaches Gesetz der großen Zahlen

Es sei A ein Ereignis, das bei einem Zufallsexperiment mit der Wahrscheinlichkeit \(\mathbb{P}(A) = p\) eintrete. Die relative Häufigkeit des Ereignisses \(A\) bei \(n\) unabhängigen Wiederholungen des Zufallsexperiments bezeichnen wir mit \(h_n\). Dann gilt für jede positive Zahl \(\epsilon\): \[\begin{align*}\lim_{n \rightarrow \infty} \mathbb{P}(|h_n-p| < \epsilon) = 1\end{align*}\] bzw. gleichwertig \[\begin{align*}\lim_{n \rightarrow \infty} \mathbb{P}(|h_n-p| \geq \epsilon) = 0\end{align*}\]

(Kütting und Sauer 2014, 280).

Dies deckt sich mit der Aussage von Büchter und Henn (2005), denn umgangssprachlich formuliert, lautet das Gesetz, wie folgt: Wenn das \(n\) wächst, so strebt die Wahrscheinlichkeit gegen 1, wenn die relativen Häufigkeiten des Ereignisses \(A\) weniger als die vorgegebene Zahl \(\epsilon < 0\) von der Wahrscheinlichkeit \(\mathbb{P}(A) = p\) abweicht (Kütting und Sauer 2014, 280).

2.2.2 Theoretischer Zugang

theoretischer ZugangIm Gegensatz zu einem empirischen Zugang, bei welchem die Wahrscheinlichkeiten nach der Durchführung des Zufallsexperiments bestimmt werden (vgl. 2.2.1 empirischer Zugang), benötigt man für die Bestimmung der Wahrscheinlichkeit für ein Ereignis keine Durchführung des Experiments – die Wahrscheinlichkeiten werden theoretisch bestimmt (Schnell 2014, 14:24). Jedoch sollten diese theoretischen Wahrscheinlichkeiten und deren Bestimmung nicht den Axiomen von Kolmogorov widersprechen (Büchter und Henn 2005, 159). Durch den theoretischen Zugang erhält man die objektive Wahrscheinlichkeit. Diese Wahrscheinlichkeitsbegriffe entwickelten sich am Anfang des 20. Jahrhunderts und basieren auf der Definition von Laplace (Schmid 2014, 5).

[Laplace-Wahrscheinlichkeit]Der theoretische Zugang, oder auch der klassische Ansatz, wird sehr häufig mit der Laplace-Wahrscheinlichkeit verknüpft, so auch bei Hauer-Typpelt (2010) und Eichler und Vogel (2009). Bei der Laplace-Wahrscheinlichkeit handelt es sich um eine Gleichwahrscheinlichkeit. Man geht von einem Zufallsexperiment mit einer endlichen Ereignissemenge \(\Omega\) aus. Dabei sollen alle Elementarereignisse gleichwahrscheinlich sein. Die Wahrscheinlichkeit \(\mathbb{P}(A)\) eines Ereignisses \(A\) berechnet sich dann durch \[\begin{align*} \mathbb{P}(A) = \frac{\text{Anzahl der Elemente von }A}{\text{Anzahl der Elemente von }\Omega} \end{align*}\]

und bedeutet, dass man die günstigen durch die möglichen Fälle dividiert (Schnell 2014, 14:24; Büchter und Henn 2005, 146). Dieser Quotient wurde bereits 11 Jahre vor der Geburt von Pierre Simon Laplace (1749 – 1827) von Abraham de Moivre (1667 – 1754) im Jahr 1738 veröffentlicht (Kütting und Sauer 2014, 86). Man spricht von einem Laplace-Experiment, wenn die Annahme der Gleichwahrscheinlichkeit sinnvoll ist. Diese Annahme kann auf theoretischen Überlegungen basieren. Ein Beispiel hierfür wäre der (faire) Würfel, welcher aufgrund der Symmetrie die Annahme der Gleichwahrscheinlichkeit sinnvoll macht (Büchter und Henn 2005, 140). Für die Einschätzung der Wahrscheinlichkeit kann folgendes Prinzip zur Geltung kommen:

Prinzip des unzureichenden Grundes

Das Prinzip des unzureichenden Grundes sagt aus, dass man am Modell der Gleichwahrscheinlichkeit von Elementarereignissen festhält, wenn man keinen Grund hat, diese Modelle anzuzweifeln (Eichler und Vogel 2011, 101).

Jedoch muss auch klar sein, dass nicht alle Ereignisse beziehungsweise Situationen mit Gleichwahrscheinlichkeit zu betrachten sind (Büchter und Henn 2005, 140). Deshalb sollte nicht die Fehlvorstellung aufkommen, dass es sich bei der Laplace-Wahrscheinlichkeit um eine Definition handelt. Diese Wahrscheinlichkeit ist eine Vorschrift zur Berechnung, welche nur bei bestimmten Bedingungen (Gleichmöglichkeit der Fälle) verwendet werden darf (Eichler und Vogel 2009, 87).

[Problematik beim klassischen Ansatz]Wie erwähnt, gibt die Laplace-Wahrscheinlichkeit keine Definition des Wahrscheinlichkeitsbegriffs. Aus diesem Grund ist die alleinige Behandlung von Laplace-Wahrscheinlichkeit nicht ausreichend. Ein weiterer Nachteil des klassischen Ansatzes ist, dass er nur für endliche Ergebnismengen anwendbar ist und sich in der Realität oft auf den Einsatz bei Glücksspielen reduziert (Eichler und Vogel 2011, 102). Die Voraussetzungen für die Anwendung des klassischen Ansatzes (Laplace-Wahrscheinlichkeit) sind: Es dürfen nur endlich viele Versuchsergebnisse möglich sein und alle Elementarereignisse müssen dieselbe Wahrscheinlichkeit besitzen. Die erste Bedingung (endliche Ereignismenge) reicht nicht aus. Aus diesem Grund ist die Laplace-Wahrscheinlichkeit nicht auf alle Zufallsexperimente mit endlichen Ereignismengen anwendbar (Bosch 2011, 13).

[Axiomatisierung]Sowohl das empirische Gesetz der großen Zahlen als auch die Laplace-Wahrscheinlichkeit liefern kein vollständiges Bild der Stochastik. Bereits im Jahr 1900 wurde von David Hilbert (1862 – 1943) der axiomatische Aufbau der Wahrscheinlichkeitstheorie gefordert. Diese Axiome wurden aber erst 1933 von Alexander Nikolajewitsch Kolmogoroff (1903 – 1987) aufgestellt. Dabei wird auch der Begriff “Wahrscheinlichkeit” beschrieben. Dies geschieht mathematisch abstrakt und ohne Bezug zu irgendwelchen Anwendungen, durch die weiteren Axiome werden die “Spielregeln” geregelt (Kütting und Sauer 2014, 89). Durch diese abstrakte Betrachtung liefert das Axiomensystem nicht unbedingt eine Grundvorstellung und sollte eher am Ende des theoretischen Zugangs mitbehandelt werden.

2.2.3 Subjektiver Zugang

[subjektivistischer Ansatz]Beim subjektivistischen Ansatz handelt sich um einen theoretischen Ansatz. Der subjektive Zugang geht – wie der Name schon sagt – von den eigenen Erfahrungen und Vorstellungen aus und ergibt eine Schätzung für die Wahrscheinlichkeit vor dem Zufallsexperiment. Damit ist aber auch verbunden, dass man aus den Erfahrungen lernt und gegebenenfalls auch diese Einschätzungen revidieren und neu aufstellen muss (Eichler und Vogel 2009, 180; Schmid 2014, 6).

[subjektive Wahrscheinlichkeit]Bei Büchter und Henn (2005) wird die subjektive Wahrscheinlichkeit als ein subjektives Maß für den persönlichen Grad der Überzeugung beschrieben. Die Wahrscheinlichkeitseinschätzung als Bewertung mit “mehr” oder “weniger wahrscheinlich” ist im besten Fall qualitativ und zumeist subjektiv. Somit stellen diese Aussagen Vermutungen dar. Die Vermutungen, welche sich nicht bestätigen, sollten verworfen, die Situation neu eingeschätzt und durch bessere ersetzt werden (Büchter und Henn 2005, 150). Eckstein (2013) definiert die subjektive Wahrscheinlichkeit wie folgt: “Die wissensbasierte Bestimmung der Wahrscheinlichkeit \(\mathbb{P}(A)\) eines zufälligen Ereignisses \(A\) durch eine Person, die mit dem jeweiligen Zufallsexperiment vertraut ist, heißt subjektive Wahrscheinlichkeit.” Hier fließt schon mit ein, dass die subjektive Wahrscheinlichkeit auf Basis von gewonnenen Informationen entsteht. Weiters wird ersichtlich, dass jede Person eine andere Einschätzung der Wahrscheinlichkeit besitzt. Es gibt die persönliche Vermutung von Person A, die persönliche Vermutung von Person B, etc. (Eckstein 2013, 168; Schmid 2014, 6).

[Gründe für subjektive Wahrscheinlichkeit]Im Mathematikunterricht geht es meist um die rationale Betrachtung von Problemen und man versucht zu zeigen, dass die Mathematik eine Fachwissenschaft ist (Hauer-Typpelt 2010, 7). In der Stochastik fließen jedoch vom ersten Moment Erfahrungen und Erwartungen ein (vgl. Primärintuitionen von Freudenthal) (Hauer-Typpelt 2010, 12). Diese subjektiven Einschätzungen kann man in der Stochastik auch nicht vollständig ausschließen. Gerade in Bereich der Kreditvergabe fließen auch Einschätzungen von ExpertInnen ein. Somit sollte die subjektive Wahrscheinlichkeit auch einen Platz im Schulunterricht finden. Nur sollte geübt werden, wie man subjektive Informationen aufnimmt und in die Berechnungen einfließen lässt (Hauer-Typpelt 2010, 7). Ein Vorteil der subjektiven Wahrscheinlichkeit ist, dass dieser auch bei nicht-wiederholbaren Zufallsexperimenten anwendbar ist. Trotz der subjektiven Komponente sollte versucht werden, möglichst rational die Vermutung über die Wahrscheinlichkeit zu begründen (Schnell 2014, 14:25).

2.3 Muster und Variabilität

[Muster im Zufall]Wenn man von einer Musterlosigkeit des Zufalls ausgeht, ist es oftmals nicht intuitiv, dass auch bei zufälligen Vorgängen Muster in den Daten erkennbar sind. Mathematische Wahrscheinlichkeiten beziehen sich gerade auf diese Muster, welche erst bei langer Sicht (häufiger Durchführung eines Zufallsexperiments) auftreten (Schnell 2014, 14:28). Bei geringer Anzahl an Durchführungen sind Muster schwer zu beobachten, oder anders gesagt: Die Ergebnisse des Zufallsexperiments weichen stark von den erwarteten Mustern ab (Schnell 2014, 14:34). Bei der Annäherung der objektiven Wahrscheinlichkeit geht es darum, dass Muster in den Ergebnissen von Zufallsexperimenten gefunden und mithilfe von Wahrscheinlichkeiten quantifiziert werden (Eichler und Vogel 2009, 169).

[Variabilität bei kurzen Serien]Die oben angesprochene Musterlosigkeit tritt oftmals bei geringer Durchführung eines Zufallsexperiments auf und wird als Variabilität betitelt. Diese Variabilität ist in empirischen Ergebnissen immer präsent. Jedoch ist die Stärke dieser Variabilität von der Anzahl der Durchführungen des Zufallsexperiments abhängig. Dies führt dann bei sehr häufiger Durchführung des Zufallsexperiments dazu, dass sich die Muster klarer herauskristallisieren (Schnell 2014, 14:28). Die Variabilität ist ein eigenständiges Phänomen, welches – wie beschrieben – die Beobachtbarkeit von Mustern ergänzt. Dieses Phänomen ist jedoch noch weniger beforscht (Schnell 2014, 14:39).

[Gesetz der kleinen Zahlen]Die Muster in den Ausgängen der Zufallsexperimente treten erst nach häufiger Durchführung des Experiments auf. Jedoch gibt es die Fehlvorstellung, dass diese Muster schon bei kurzen Serien erwartet werden. Dies geschieht vor allem, wenn die theoretische Wahrscheinlichkeit für dieses Ereignis bereits bekannt ist. Diese Mustererwartung wird als Repräsentativitätsheuristik bezeichnet. Da es keine Berücksichtigung der Anzahl der Durchführungen des Zufallsexperiments gibt, spricht man unter anderem vom “Gesetz der kleinen Zahlen.” Generell sollte man diese Vorstellung nicht außer acht lassen, da diese ausbaufähige Aspekte beinhaltet. Positiv bei der Repräsentativitätsheuristik ist, dass Muster erwartet werden. Weiters werden nicht nur einzelne Ausgänge betrachtet, sondern die gesamte Serie. Ein Nachteil der Repräsentativitätsheuristik ist jedoch, dass die Anzahl der Experimentsdurchführungen nicht beachtet wird (Schnell 2014, 14:35).

[Beispiel Variabilität]Als Beispiel für die Enttäuschung der Mustererwartung kann man ein Münzspiel betrachten. Dabei handelt es sich um eine faire Münze und die Wahrscheinlichkeit, dass diese auf Kopf landet, liegt bei \(\mathbb{P}("\text{Kopf}")=\frac{1}{2}\). Die Münze wird 20 Mal geworfen und die relative Häufigkeit für das Ereignis “Kopf” berechnet. Um die Variabilität zu verdeutlichen, wird diese 20er-Serie insgesamt 50 mal wiederholt. In Abb. 2.2 sind diese relativen Häufigkeiten, sowie die theoretische Wahrscheinlichkeit (blau eingezeichnet) zu finden. Es ist ersichtlich, dass bei einer so kurzen Serie größere Abweichungen von der erwarteten relativen Häufigkeit von \(\frac{1}{2}\) auftreten.

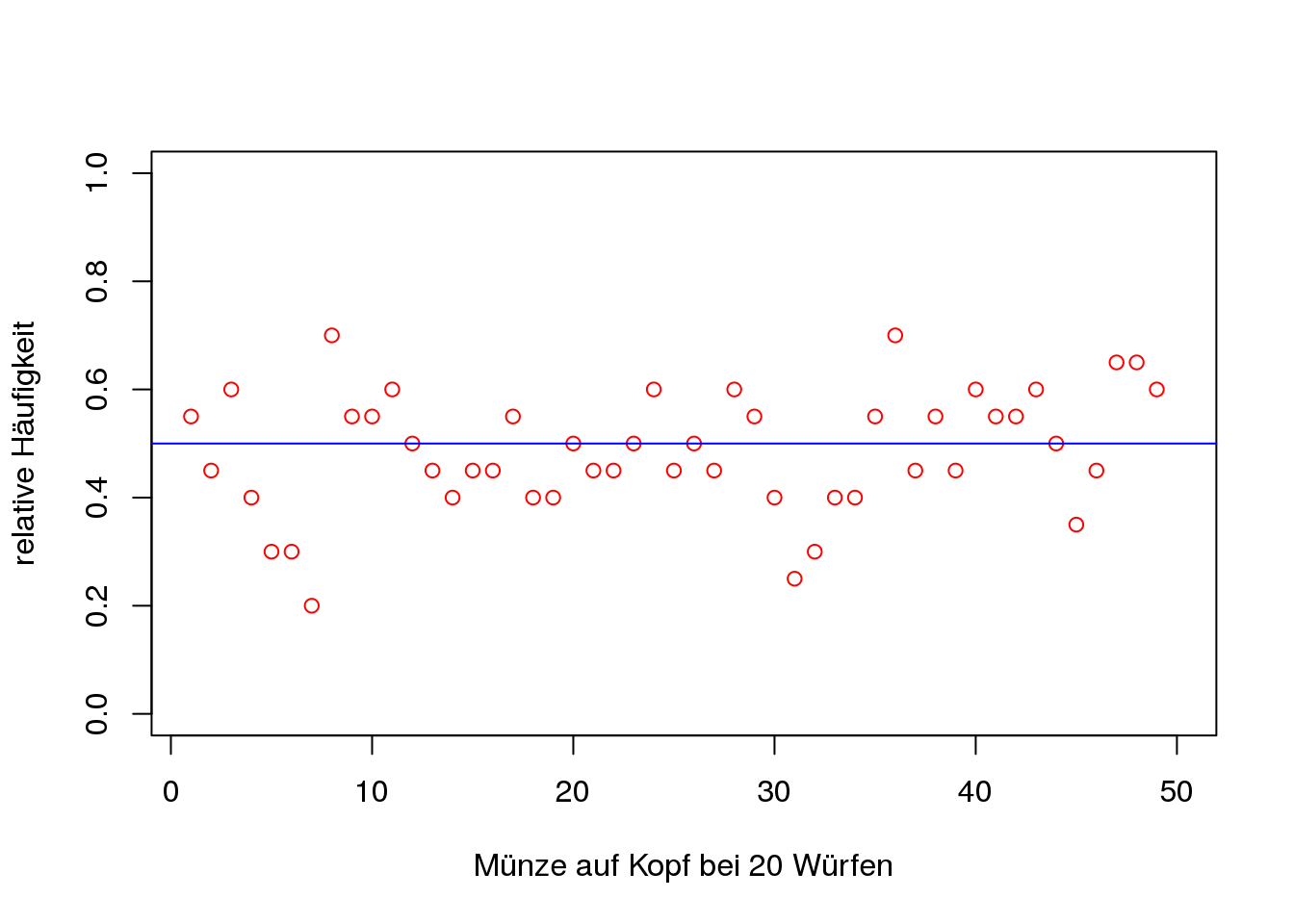
Figure 2.2: Musterenttäuschung bei kurzen Serien eines Münzwurfs

[empirisches Gesetz der großen Zahlen]Während beim Gesetz der kleinen Zahlen die Anzahl der Versuchswiederholungen nicht berücksichtigt werden, wird die Anzahl in die Überlegungen einbezogen, wenn das empirische Gesetz der großen Zahlen (vgl. 2.2.1 empirischer Zugang) bekannt ist (Schnell 2014, 14:37). Aspinwall und Tarr (2001) wollen in ihrer Studie zeigen, ob SchülerInnen die “ability to make a connection between the experimental probability of an event (using relative frequencies to determine the likelihood of an event) and the theoretical probability of an event (derived analytically)” haben. Dieser Zusammenhang soll mit dem empirischen Gesetz der großen Zahlen gelingen. In der Studie zeigen Aspinwall und Tarr, dass es möglich ist, dass SchülerInnen aus der sechsten Jahrgangsstufe die Mustererwartung an die Anzahl der Versuchswiederholungen anpassen. Zunächst fielen die SchülerInnen in die Repräsentativitätsheuristik. Nach dem Kennenlernen des empirischen Gesetzes der großen Zahlen passten sie ihre Mustererwartung an (Aspinwall und Tarr 2001, 15).

[Beispiel Mustererwartung]Mithilfe des empirischen Gesetzes der großen Zahlen kann man die Mustererwartung bei häufiger Durchführung erkennen. Nun kann das Beispiel des Münzspiels mit einer fairen Münze (\(\mathbb{P}("\text{Kopf}")=\frac{1}{2}\)) auf lange Sicht betrachtet werden. Dazu wurde die Münze einmal, zweimal, dreimal… geworfen, die relative Häufigkeit für das Ereignis “Kopf” berechnet und geplottet (vgl. Abb. 2.3). Wiederum ist die theoretische Wahrscheinlichkeit in blau eingezeichnet. Die Stabilisierung der relativen Häufigkeiten ist bei zunehmender Anzahl der betrachteten Münzwürfe ersichtlich.

Figure 2.3: empirisches Gesetz der großen Zahlen anhand eines Münzwurfs

[Variabilität ist Zufall?]Während bei der Repräsentativitätsheuristik die Muster erwartet werden, sehen viele SchülerInnen die Abwesenheit von Mustern als Zeichen für den “Zufall” an. Das bedeutet, dass die Variabilität als Indikator für den Zufall herangezogen wird. Durch diese Überlegung würden Muster und Zufall sich gegenseitig ausschließen. Probleme treten bei dieser Vorstellung auf, wenn Zufallsexperimente auf lange Sicht betrachtet werden (Schnell 2014, 14:41).

[Teil des statistischen Denkens]Von Wild und Pfannkuch (1999) werden insgesamt fünf Aspekte des statistischen Denkens beschrieben. Dabei fließen auch Muster und Variabilität als zentrale Elemente ein. So wird als ein Aspekt des statistischen Denkens, die Einsicht in die Variabilität statistischer Daten (consideration of variation) genannt. Damit wird gemeint, dass die Ergebnisse von Umfragen, Experimenten, etc. nicht genau vorauszusagen sind. Aber auch, dass beispielsweise Umfrageergebnisse an verschiedenen Tagen anders ausfallen. Es kommt zu einer Non-Uniformität der Ergebnisse verschiedener statistischer Erhebungen. Ein weiterer Aspekt ist das Erkennen von Mustern in den Daten und deren Beschreibung mit statistischen Modellen (reasoning with statistical models). Hier soll deutlich werden, dass trotz der vorhandenen Variabilität Muster in den Daten möglich sind (Wild und Pfannkuch 1999, 226; Eichler und Vogel 2009, 11).

[variation messages]Die Variabilität (variation oder variability) ist ein zentraler Aspekt für das statistische Denken. Die Variabilität geht mit einigen Aspekten einher. Wild und Pfannkuch (1999) betiteln diese als variation messages. Die ersten drei Nachrichten sind: variation is omnipresent; variation can have serious practical consequences; and statistics give us a means of understanding a variation-beset wordl (Wild und Pfannkuch 1999, 235). Die erste dieser Nachrichten ist für die Stochastik eine nähere Betrachtung wert.

[Omnipräsenz]Variabilität ist omnipräsent und kann in der Realität (Umfragen, Würfelergebnisse, etc.) beobachtet werden: “It is present everywhere and in everything”. Im realen Leben ist es schwer, zwei vollkommen identische Vorgehen, Bewegungsabläufe oder Werkstücke zu finden. Die Variabilität ist somit nicht nur Bestandteil der Stochastik, sondern begegnet uns immer (Wild und Pfannkuch 1999, 235).