Kapitel 3 Stufenmodell

Bereits von Riemer (1991) wurde ein Stufenmodell für den intuitiven Zugang zu Konfidenzintervallen vorgestellt. Ein weiteres Stufenmodell wurde von Biehler und Prömmel (2013) beschrieben. Dieses Stufenmodell wird im folgenden Kapitel näher beleuchtet. Bei diesem Modell werden unterschiedliche Schritte zum intuitiven Zugang zu Konfidenzintervallen anhand des Münzwurfes betrachtet. Der Münzwurf ist eines der klassischen Beispiele in der Stochastik, wie schon Freudenthal (1972) erwähnte. Das behandelte Stufenmodell sollte von einer Simulation begleitet werden.

[Einsatz des Stufenmodells]Das Stufenkonzept von Biehler und Prömmel kann in unterschiedlichen Klassenstufen zum Einsatz kommen. Generell ist es dazu gedacht in den Schulstufen 6 bis 12 verwendet zu werden. Um Grundvorstellungen zu Zufall und Wahrscheinlichkeit – und somit eine stochastische Allgemeinbildung – auszubilden, kann auch vor der Sekundarstufe II mit der Behandlung dieser Themen begonnen werden. Beispielsweise ist das Verstehen des \(1/\sqrt{n}\)-Gesetzes für die spätere Behandlung der Konfidenzintervalle von Bedeutung. Das Kennenlernen des Gesetzes der großen Zahlen kann als Vorbereitung dafür gesehen werden (Biehler und Prömmel 2013, 14).

[mathematischer Hintergrund]Als mathematische Grundlagen hinter dem Stufenkonzept steht die Hinführung zum Konfidenzintervall über das empirische Gesetz der großen Zahlen. So soll zunächst ein Gefühl für die Variabilität und Musterbildung bei den Ergebnissen der Zufallsexperimente vermittelt werden. Diese Musterbildung wird mit dem empirischen Gesetz der großen Zahlen in Verbindung gebracht. Das \(1/\sqrt{n}\)-Gesetz gilt als Abschätzungssatz für endliche Durchführungen des Zufallsexperiments. Nach der Behandlung von Prognoseintervallen können dann auch Konfidenzintervalle dargelegt werden (Prömmel 2013, 67).

[Entwicklung des Modells]Das Stufenkonzept ist stark mit dem empirischen Gesetz der großen Zahlen verknüpft und basiert auf einer Untersuchung, ob Lernende die Stichprobengröße bei konkreten Zufallsexperimenten miteinbeziehen und diese mit einer intuitiven Vorstellung des empirischen Gesetzes der großen Zahlen verknüpfen. Die Untersuchung ergab, dass die meisten SchülerInnen eine schwache Intuition zum Gesetz der großen Zahlen haben (Biehler und Prömmel 2013, 15f). Bereits in früheren Untersuchungen wurde entdeckt, dass viele Menschen an ein Gesetz der kleinen Zahlen glauben. Das heißt, diese Personen nehmen fälschlicherweise an, dass sich bereits bei geringen Stichprobenumfängen Muster einstellen, sprich, die relative Häufigkeit nahe der theoretischen Häufigkeit ist (Kahneman und Tversky 1982, 131; Sedlmeier und Gigerenzer 1997, 34). Um eine tragfähige Vorstellung zum empirischen Gesetz der großen Zahlen zu erhalten, wurde das Stufenkonzept für den Unterricht entwickelt (Biehler und Prömmel 2013, 17).

3.1 Schwankungsvergleiche für zwei verschiedene \(n\)

[Ausgangssituation]Wie erwähnt, baut das Stufenmodell auf dem Münzwurf auf. Dabei soll beim Münzwurf das Ereignis “Kopf” näher analysiert werden. Beim Schwankungsvergleich für zwei verschiedene \(n\) werden zwei verschiedene Serien des Münzwurfes gegenübergestellt. Eine der Serien betrachtet nur eine geringe Anzahl an Münzwürfen, die andere Serie soll eine höhere Münzwurfanzahl visualisieren. Das Ziel ist, dass die Schwankungen der relativen Häufigkeiten der beiden Serien näher betrachtet werden (Biehler und Prömmel 2013, 18).

[Erkennen von Variabilität]Durch das Betrachten der relativen Häufigkeiten für das Ereignis “Kopf” soll die Variabilität herausgestrichen werden. Dabei sollen die Schwankungen der relativen Häufigkeiten bei geringen Stichprobenumfängen (kleinen \(n\)) mit der omnipräsenten Variabilität (vgl. 2.3 Muster und Variabilität) in Verbindung gebracht werden. Somit werden die möglichen Fehlvorstellungen zu den Schwankungen am Beginn explizit behandelt.

[Stabilisierung der absoluten Häufigkeit?]Im Stufenmodell von Biehler und Prömmel (2013) werden nicht nur die relativen, sondern auch die absoluten Häufigkeiten betrachtet und somit auch die Schwankungen in beiden Fällen. Die Schwankungen der absoluten Häufigkeit für größere Stichprobenumfänge werden durch die Abweichungen vom Erwartungswert \(n/2\) visualisiert (Biehler und Prömmel 2013, 19). Die Fehlvorstellung einer Stabilisierung der absoluten Häufigkeiten – entsprechend dem empirischen Gesetz der großen Zahlen für relative Häufigkeiten – ist weit verbreitet. In diesem Fall nimmt man fälschlicherweise an, dass bei einer Wahrscheinlichkeit \(p = 0,5\) bei \(n\) Würfen \(n/2\)-mal Kopf geworfen wird, wenn \(n\) möglichst groß ist. In diesem Beispiel (vgl. Abb. 3.1) ist erkennbar, dass die Differenz der absoluten Häufigkeiten vom Erwartungswert \(n/2\) stark abweicht.

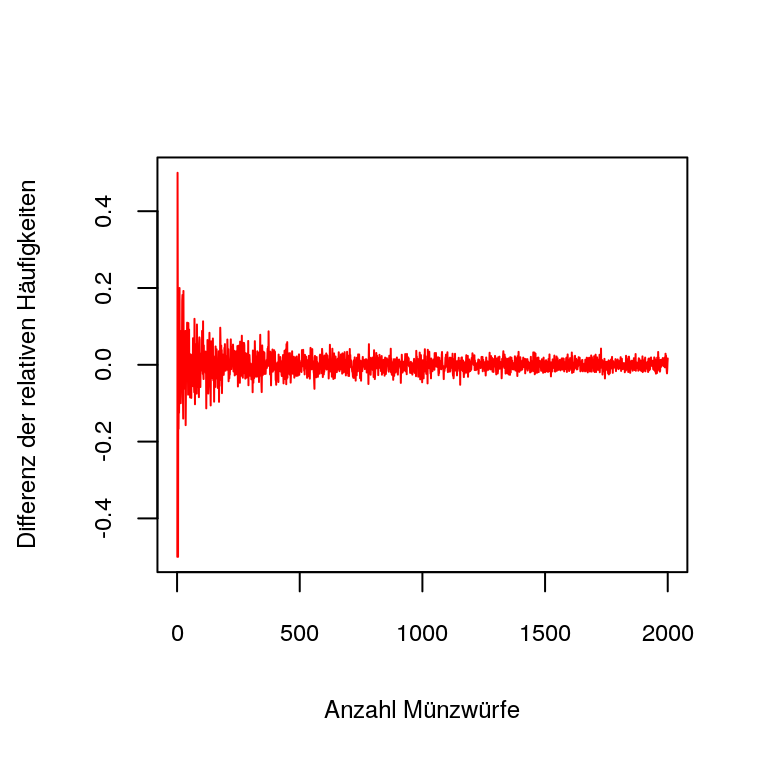
Figure 3.1: Vergleich der Differenz der absoluten und relativen Häufikgeit zum Erwartungswert

[Muster in den Serien]Weiters werden in dieser Stufe schon Ansätze in der Mustererkennung benötigt, da die zweite Serie einen größeren Stichprobenumfang (größeres \(n\)) besitzt. Diese Muster treten vor allem bei den relativen Häufigkeiten auf, wie es im Plot zu sehen ist. Hier wird ersichtlich, dass die Differenz zwischen den relativen Häufigkeiten und dem Erwartungswert 0.5 einer fairen Münze kleiner wird. Auch im Stufenkonzept von Riemer (1991) werden diese Schwankungen betrachtet. Er nennt diesen Punkt Experimentelle Untersuchung von Zufallsschwankungen, was die Bedeutung der durch Variabilität bedingten Schwankungen unterstreicht.

3.2 Entwicklung für wachsendes \(n\)

[Ausgangssituation]Auch in dieser Stufe geht man von einem Münzwurf aus und analysiert das Ereignis “Kopf”. Im Gegensatz zur ersten Stufe werden nicht zwei verschiedene Serien einander gegenübergestellt, sondern eine Serie auf längere Sicht betrachtet. Das Ziel ist, dass die Stabilisierungen der relativen Häufigkeiten – auch bei Wiederholungen des Experiments – beobachtet werden. Dabei betrachtet man die Entwicklung für wachsendes \(n\) aus verschiedenen Perspektiven (Biehler und Prömmel 2013, 19).

[Näherungsprozess]Der erste Aspekt, welcher beobachtet werden sollte, ist der Näherungsprozess der relativen Häufigkeiten (Biehler und Prömmel 2013, 19). Dieser Näherungsprozess ist ein Muster, welches sich auf lange Sicht herauskristallisiert. Dieser Näherungsprozess ist stark mit dem empirischen Gesetz der großen Zahlen verwoben. Damit soll ausgesagt werden, dass sich die relativen Häufigkeiten bei häufiger Durchführung eines Zufallsexperiments um einen bestimmten Wert – zumeist der theoretischen Wahrscheinlichkeit – stabilisieren. Diese Stabilisierung tritt nur bei einem größeren \(n\) ein, bei geringen Versuchswiederholungen ist die bereits in der vorherigen Stufe erwähnte Variabilität zu finden (Schnell 2014, 14:16). Auch im 1991 entwickelten Stufenmodell von Riemer fließt dieser Näherungsprozess implizit im Schritt 2: Experimentelle Untersuchung von Zufallsschwankungen ein (Riemer 1991, 26).

[relative und absolute Abweichung]Die relativen und absoluten Abweichungen vom Erwartungswert sind ein weiterer Aspekt dieser Stufe. Dabei legen Biehler und Prömmel (2013) das Augenmerk darauf, dass diese beiden Abweichungen simultan erforscht werden können. Die Simulation hat hier den Vorteil, dass diese Stabilisierung der relativen Häufigkeiten immer wieder – trotz neuer Zufallsexperimente – beobachtet werden kann (Biehler und Prömmel 2013, 19). Mathematisch steht das empirische Gesetz der großen Zahlen im Hintergrund der Stabilisierung der relativen Häufigkeiten beziehungsweise der relativen Abweichung vom Erwartungswert (Schnell 2014, 14:16). Das Erkennen dieser Stabilisierung und die Verbindung zum empirischen Gesetz der großen Zahlen kann “eine wichtige Grundlage beim Aufbau tragfähiger, stochastischer Vorstellungen darstellen” (Schnell 2014, 14:23). Das schwache Gesetz der großen Zahlen, oder besser gesagt der Spezialfall des Bernoulli-Theorems, liefert die mathematische Begründung, dass bei hoher Versuchsanzahl die relativen Häufigkeiten nahe der theoretischen Wahrscheinlichkeit liegen (Prömmel 2013, 70). Um der Fehlvorstellung des Gesetzes der kleinen Zahlen entgegenzuwirken, werden die absoluten Abweichungen vom Erwartungswert \(n/2\) noch einmal aufgegriffen und visualisiert (Biehler und Prömmel 2013, 17+19).

[bessere Annäherung bei höherem n]Um den Fokus nochmals und explizit auf die Stichprobengröße zu legen, werden die relativen Häufigkeiten von drei Stichproben, mit unterschiedlichem Stichprobenumfang (\(n = 50, 200, 1000\)) visualisiert. Durch diese Simulation ist es möglich zu beobachten, dass bei größeren \(n\) die relativen Häufigkeiten sich mehr um die theoretische Wahrscheinlichkeit stabilisieren, als bei kleinen \(n\) (Biehler und Prömmel 2013, 19). Hier spielen auch wieder Muster und Variabilität eine Rolle und fassen somit die ersten zwei Stufen noch zusammen (Schnell 2014, 14:34f).

[sample size effect]In dieser Stufe werden explizit der Stichprobenumfang und die abnehmende Variabilität bei größeren Stichprobenumfängen beleuchtet (Biehler und Prömmel 2013, 16). Bereits Bernoulli schrieb in einen Brief an Leibnitz, dass “‘even the stupidest man knows by some instinct of nature per se and by no previous instruction’ that the greater the number of confirming observations, the surer the conjecture” (Sedlmeier und Gigerenzer 1997, 33). Das Einbeziehen des Stichprobenumfangs wird auch als sample size effect bezeichnet. Die alleinige Vorstellung, dass sich die relativen Häufigkeiten auf lange Sicht um die theoretischen Wahrscheinlichkeiten stabilisieren, reicht für die stochastische Allgemeinbildung nicht aus. In den meisten Fällen liegt ein endlicher Stichprobenumfang vor, welcher Basis für die weiteren Schlüsse ist. Aus diesem Grund müssen Grundvorstellungen zu den folgenden Punkten entwickelt werden:

• Wie groß sind die Schwankungen der relativen Häufigkeiten um die Wahrscheinlichkeiten bei einem fest gewählten Stichprobenumfang \(n\)?
• Wie sieht die Abnahme der beobachtbaren Variation bei wachsendem Stichprobenumfang \(n\) aus?

Diese Grundvorstellungen sind komplex, da “[man sich] zu jedem festen Stichprobenumfang \(n\) […] eine Verteilung der relativen Häufigkeiten vorstellen [muss], deren ‘Streuung’ dann mit wachsendem \(n\) abnimmt” (Biehler und Prömmel 2013, 16f).

3.3 Variation bei wachsendem \(n\)

[Ausgangssituation]Wiederum wird das Ereignis “Kopf” eines mehrfachen Münzwurfes betrachtet. In dieser Stufe werden mehrere längere Serien des Münzwurfes beleuchtet, sodass trotz der Musterbildung die Variation bei einem wachsenden Stichprobenumfang \(n\) deutlich wird. Um dieser Variation auf den Grund zu gehen, nähert man sich dem Phänomen aus verschiedenen Blickwinkeln (Biehler und Prömmel 2013, 20).

[Gruppierung um Wahrscheinlichkeit]Die erste Perspektive betrachtet die Variation bei wachsendem \(n\) auf globale Weise. Anstatt nur eine Serie des Münzwurfes zu betrachten, werden mehrere Trajektoren (Bahnkurven) des Münzwurfes visualisiert. Dadurch ist einerseits die abnehmende Variation bei wachsendem \(n\) pro Münzwurfserie und andererseits die Variation zwischen den einzelnen Serien (Biehler und Prömmel 2013, 20). Dies kann beispielsweise wie folgt aussehen:

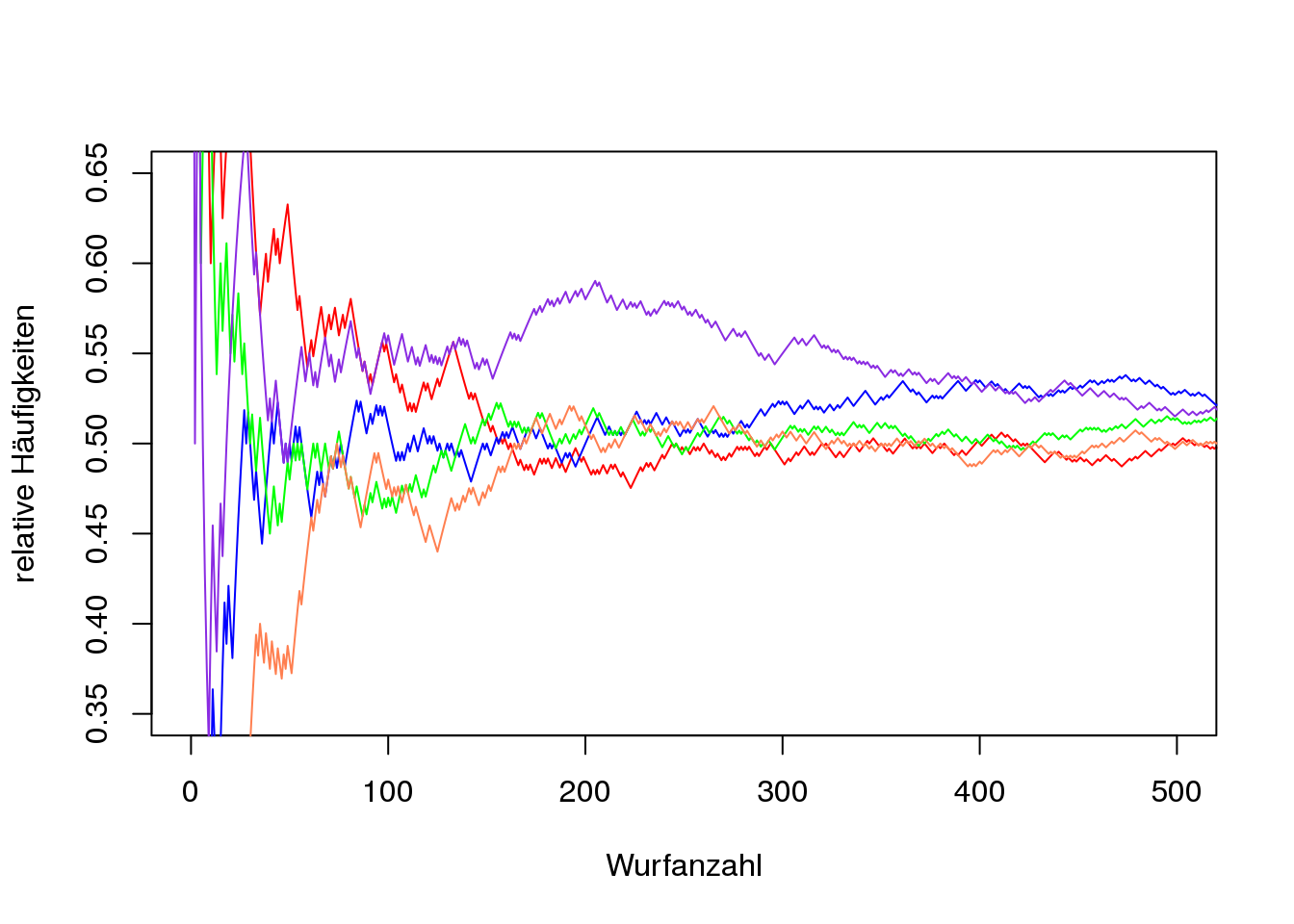
Figure 3.2: Münzwurfserien im Vergleich

[tabellarische Darstellung]Um mit diesen Beobachtungen weiterarbeiten zu können, werden jeweils die fünf relativen Häufigkeiten der Serien beim Münzwurf \(n\) zusätzlich mithilfe einer Tabelle dargestellt. Wenn man dieses Experiment beispielsweise fünfmal wiederholt, erhält man mehr Daten für die Ausarbeitung. Um auch hier wieder den Bezug zwischen langer und kurzer Sicht darzustellen, werden sowohl die Werte von \(n = 50\) als auch von \(n = 200\) dargestellt (Biehler und Prömmel 2013, 20). Im Vergleich zwischen \(n = 50\) und \(n = 100\) erkennt man, dass bei einem höheren Stichprobenumfang die relativen Häufigkeiten nicht mehr so stark um die theoretische Wahrscheinlichkeit schwanken. Somit wird wieder der Blick auf den Stichprobenumfang gelegt, um Fehlvorstellungen vorzubeugen. Eine Studie aus dem Jahr 2001 ergab, dass “five of six case study students demonstrated limited awareness of the relationship between experimental probability and the number of trials in an experiment.”(Aspinwall und Tarr 2001, 233) Somit sollte die Vorbeugung beziehungsweise Behandlung dieser Fehlvorstellung nicht zu kurz kommen.

[Darstellung mit Punktdiagramm]Um eine weitere Darstellungsart anzubieten, werden diese Daten noch in einem Punktdiagramm dargestellt. Hier ist klar erkenntlich, dass sich die relativen Häufigkeiten bei einer höheren Stichprobengröße mehr um die theoretische Wahrscheinlichkeit (\(p = 0,5\) bei einer fairen Münze) gruppieren (Biehler und Prömmel 2013, 20).

[Vorhersage der relativen Häufigkeiten]Eine offene Frage ist noch, welche Ergebnisse für die relativen Häufigkeiten für das Ereignis “Kopf” theoretisch möglich sind. Angenommen der fünfzigfache Münzwurf wird betrachtet, dann sind alle Brüche \(0/50, 1/50 \dots 50/50\) möglich. Bei der Betrachtung des zweihundertfachen Münzwurfs sogar alle Brüche von \(0/200, 1/200 \dots 200/200\). Die Wahrscheinlichkeit beim fünfzigfachen Münzwurf genau fünfzigmal “Kopf” zu erhalten, liegt bei \((1/2)^{50}\). Dies ergibt sich durch die Binomialverteilung, denn das Experiment Münzwurf wird \(n = 50\) mal unabhängig und ident durchgeführt und es wird nach dem \(k\)-maligen Erfolg (\(k=50\) für Kopf) gefragt. Somit: \[\begin{align*} p_k &= \binom{n}{k} \cdot p^k \cdot (1-p)^{n-k}\\ p_{50} &= \binom{50}{50} \cdot (\frac{1}{2})^{50} \cdot (1-(\frac{1}{2}))^{50-50} = (\frac{1}{2})^{50} \end{align*}\]

(Bosch 2011, 37) Deshalb ist eine wichtige Einsicht in dieser Stufe, dass man die relativen Häufigkeiten nicht genau vorhersagen kann. Man kann aber mit absoluter Sicherheit sagen, dass die relativen Häufigkeiten im Intervall \([0;1]\) liegen (Biehler und Prömmel 2013, 21).

[Bereiche für relative Häufigkeiten]Diese Aussage über die relativen Häufigkeiten lässt sich also sicher aufstellen, jedoch ist es sehr weit gefasst, wenn man nur das Intervall von [0;1] angibt. In der Praxis ist es deshalb auch interessant, in welchem Bereich um die theoretische Wahrscheinlichkeit sich die relativen Häufigkeiten mit 95% oder 99% aufhalten. Im Münzspiel würde man sich fragen, in welchem Bereich um \(1/2\) die relativen Häufigkeiten mit 95%-iger oder 99%-iger Wahrscheinlichkeit zu finden sind. Für die Beantwortung dieser Frage ist es nicht ausreichend, geringe Durchgänge des Zufallsexperiments zu betrachten. Erst nach sehr vielen Durchgängen kann man ermitteln, wo sich die mittleren 95% (oder 99%) der Ergebnisse aufhalten. Somit liegt ein Fokus dieser Stufe auf der Betrachtung solcher Bereiche. Diese Bereiche können betrachtet werden, wenn der fünfzigfache Münzwurf und der zweihundertfache Münzwurf jeweils 1000 Mal wiederholt wird und die mittleren 95% der Ergebnisse betrachtet werden (vgl. Abb. 3.3). Auch hier ist wieder die größere Konzentration der Werte um die theoretische Wahrscheinlichkeit \(p = 0{,}5\) beim zweihundertfachen Münzwurf zu finden (Biehler und Prömmel 2013, 21).

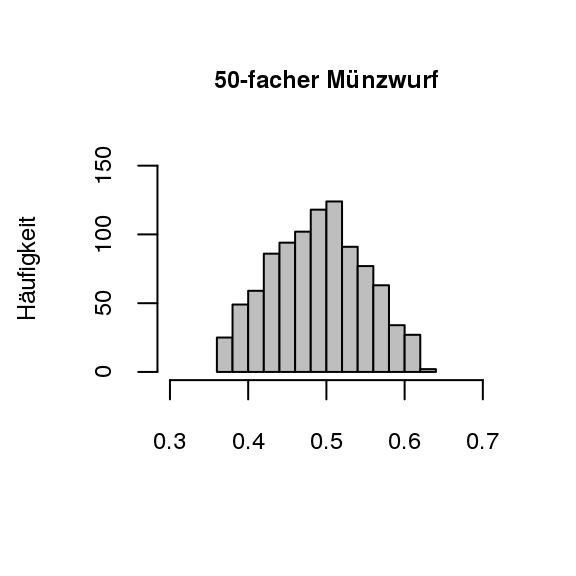
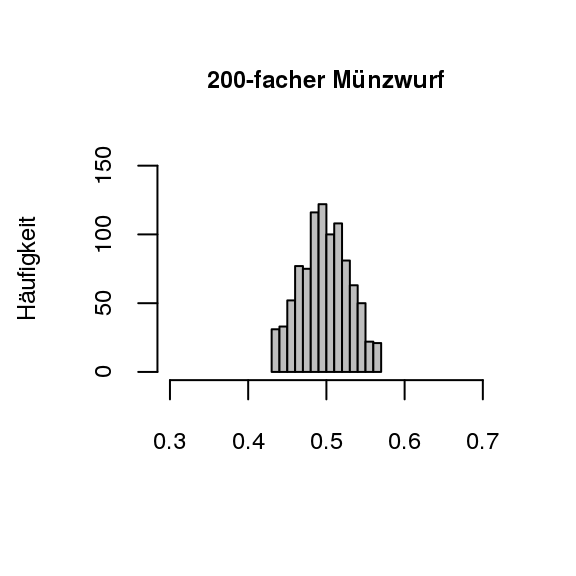
Figure 3.3: Münzwürfe im Vergleich (1000 Versuchswiederholungen)

Die höhere Konzentration um \(0,5\) beim zweihundertfachen Münzwurf ist deutlich erkennbar. Für einen direkten visuellen Vergleich wurden die beiden Grafiken identisch skaliert (Biehler und Prömmel 2013, 21). Diese Idee soll auch bei einer Simulation eingesetzt werden, sodass die Konzentration bei höherem Stichprobenumfang im Fokus bleibt und nicht das Ablesen von Diagrammen.

[Prognoseintervall ermitteln]Nach diesem visuellen Vergleich wird der Fokus noch auf den Bereich um \(0,5\) herum gelegt, in welchen die mittleren 95% der relativen Häufigkeiten für “Kopf” fallen, mathematisch (symbolisch) betrachtet. Dazu werden 1000 Stichproben der beiden Münzwurfserien genauer betrachtet. Da es sich um einen symmetrischen Bereich handelt, werden die 25 größten (\(2,5\%\)) und die 25 kleinsten (\(2,5\%\)) aus unseren Werten entfernt. Das resultierende Intervall der mittleren 95% der Daten bleibt nun übrig (Biehler und Prömmel 2013, 21). Diesen Vorgang kann man sich beim fünfzigfachen Münzwurf wie in Abb. 3.4 vorstellen.

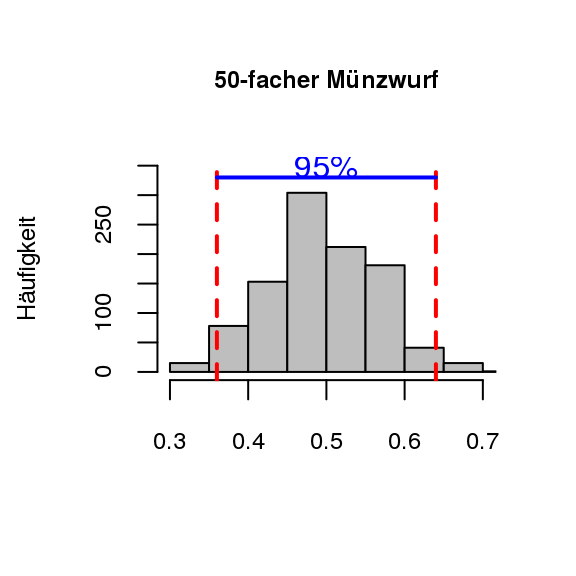
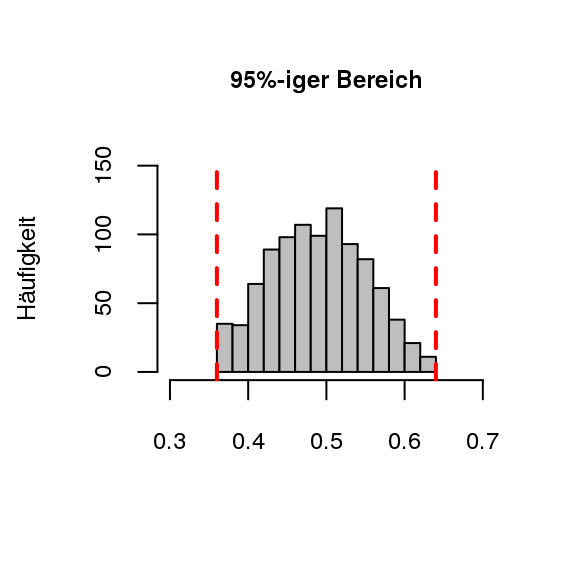
Figure 3.4: Münzwurf mit mittleren Bereich

Gerade bei diesem Beispiel sind die heutigen modernen Softwares mit ihren graphischen Möglichkeiten von Vorteil. Auch Riemer (1991) verwendet solche Intervalle (Schwankungsintervalle) in seinem Stufenmodell, jedoch standen ihm noch keine grafischen Visualisierungsmöglichkeiten zur Verfügung, weshalb er die Intervalle in tabellarischer Form behandelte.

[Quantil]Wenn Software genutzt wird, kann das Intervall mithilfe des \(2,5\%\)- und des \(97,5\%\)-Perzentils beziehungsweise Quantils der Häufigkeitsverteilung bestimmt werden (Biehler und Prömmel 2013, 21).

\(\alpha\)-Quantil

Es sei die geordente Messreihe \(x_1 \leq x_2 \leq x_3 \leq \dots \leq x_n\) gegeben. Eine Zahl \(x_{\alpha} \in \mathbb{R}\) heißt \(\alpha\)-Quantil, falls gilt: Mindestens \(\alpha \cdot 100\%\) der Daten sind kleiner oder gleich \(x_{\alpha}\) und mindestens \((1-\alpha) \cdot 100\%\) der Daten sind größer oder gleich \(x_{\alpha}\) (Kütting und Sauer 2014, 43).

Die Schwierigkeit liegt nun darin, das \(\alpha\)-Quantil so zu wählen, dass dieser Definition Genüge getan wird. Aus diesem Grund ist es im allgemeinen auch schwierig, exakt \(2,5\%\) abzuteilen (Biehler und Prömmel 2013, 21).

[Prognoseintervall]Bis dato wurde vom Bereich um die theoretische Wahrscheinlichkeit, in welchem die mittleren \(95\%\) oder \(99\%\) der relativen Häufigkeiten zu finden sind, gesprochen. Da dies eher umständlich zu sagen ist, kann man es dazu gekürzt \(95\%\)- oder \(99\%\)-Prognoseintervall nennen. Dabei kann die Breite des Prognoseintervalls als Streuungsmaß angesehen werden. Wenn man das Prognoseintervall auf diese Weise bestimmt, wird noch nicht der Begriff der \(\sigma\)-Umgebung benötigt (Biehler und Prömmel 2013, 21; Prömmel 2013, 67).

3.4 \(\frac{1}{\sqrt{n}}\)-Gesetz empirisch

[Ausgangssituation]Diese Stufe wartet nicht mit einem anderen Experiment auf, sondern betrachtet wiederum den Münzwurf – und das Ereignis “Kopf”. Die Kernfrage ist, wie die Streubreite (zum Beispiel \(95\%\)-Streubreite) vom Stichprobenumfang \(n\) abhängt. Somit werden die Stufen “Entwicklung für wachsendes \(n\)” und “Variation bei wachsendem \(n\)” miteinander in Verbindung gebracht (Biehler und Prömmel 2013, 21).

[Überprüfen auf Gesetzmäßigkeiten]Die Abhängigkeit von Streubreite und Stichprobenumfang kann anhand von Beispielen entdeckt beziehungsweise beobachtet werden.

Aus diesem Grund wird wieder der fünfzigfache und der zweihundertfache Münzwurf gegenübergestellt. Einerseits ist eine deutlich verringerte Streubreite beim Münzwurf mit dem höheren Stichprobenumfang zu erkennen. Andererseits hat sich bei der Vervierfachung des Stichprobenumfangs die \(95\%\)-Streubreite circa halbiert. Nun stellt sich die Frage, ob diese Gesetzmäßigkeit eine allgemeine Gültigkeit hat oder nur durch ein - wie von Schefcik (2009) genanntes – pathologisches Beispiel entstand (Biehler und Prömmel 2013, 21).

[Schritt zur allgemeinen Gültigkeit]Um sich der allgemeinen Gültigkeit dieser Aussage zu nähern, wird der Münzwurf für verschiedene Stichprobenumfänge \(n\) mit je 2000 Wiederholungen simuliert. Die \(95\%\)-Prognoseintervalle – der relativen Häufigkeiten für das Ereignis “Kopf” – zu jedem Stichprobenumfang werden visualisiert. Diese Veranschaulichung wird durch eine tabellarische Darstellung der jeweiligen Intervallbreiten zu jedem Stichprobenumfang \(n\) unterstützt. Zusätzlich wird der Stichprobenumfang \(n\) in Abhängigkeit von \(n\) in einem Streudiagramm geplottet. Mithilfe dieser verschiedenen grafischen Visualisierungen können SchülerInnen die Aussage, dass bei Vervierfachung des Stichprobenumfangs die \(95\%\)-Streubreite halbiert wird, empirisch überprüfen (Biehler und Prömmel 2013, 21; Prömmel 2013, 215).

[funktionaler Zusammenhang im Streudiagramm]Da der Stichprobenumfang \(n\) in Abhängigkeit von \(n\) geplottet wird, stellt sich die Frage, welche Funktion diesen Sachverhalt am besten modelliert. Oder anders formuliert, welche “Funktion diese Kovariationseigenschaft erfüllt” (vgl. Biehler und Prömmel 2013, 22; Leuders und Prediger 2005; Vollrath 1989). Diese Frage wurde auch von Prömmel (2013) an SchülerInnen gestellt, diese meinten, dass es etwas mit k durch n zu tun habe (Prömmel 2013, 216). Jedoch erkennt man, dass bei der Variation von \(k\) keine gute Approximation an die vorgegebenen Punkte stattfindet. Ein weiteres Problem dieser Überlegung ist, dass bei der Vervierfachung von \(n\) der Funktionswert geviertelt und nicht halbiert wird. Somit muss die Funktion angepasst werden und zwar wird die Überlegung \(k/n\) mit \(k/\sqrt{n}\) ausgetauscht. Mithilfe einer Simulation lässt sich dann die zu den Daten passende Funktion \(2/\sqrt{n}\) finden (Biehler und Prömmel 2013, 22).

[Faustregeln zur Streubreite]Es lässt sich mathematisch herleiten, dass die \(95\%\)-Streubreite durch \(2/\sqrt{n}\) berechnet werden kann. Dies nennt man auch das \(1/\sqrt{n}\)-Gesetz. Die bekannten Faustregeln für die \(95\%\)-Streubreite ergeben sich aus diesem Gesetz.

Stichprobenumfang \(n\)	\(95\%\)-Streubreite	Radius der mittl. \(95\%\)
50	0,28	0,14
100	0,20	0,10
1000	0,06	0,03
10000	0,02	0,01

Die Faustregeln kann man vorsichtig auch als Umkehrung für “intuitive Konfidenzintervalle” nutzen. Wenn beispielsweise eine relative Häufigkeit von \(60\%\) für ein bestimmtes Ereignis bei einem Stichprobenumfang von \(1000\) vorliegt, kann man die unbekannte Wahrscheinlichkeit – mithilfe der Werte aus der Tabelle – als \(0,60 \pm 0,03\) schätzen (Biehler und Prömmel 2013, 22).

[Fehlvorstellung zur absoluten Häufigkeit]Bereits in einer der vorigen Stufen wurde visualisiert, dass sich die absoluten Häufigkeiten nicht dem Erwartungswert \(n/2\) annähern. Dies steht im Gegensatz zu den relativen Häufigkeiten (vgl. empirisches Gesetz der großen Zahlen in 2.2.1 empirischer Zugang). Der Aspekt der nicht vorhandenen Stabilisation der absoluten Häufigkeiten soll nun parallel zu der Vorstellung zu den Schwankungen der relativen Häufigkeiten ausgebildet und verfeinert werden. Diese Vorstellung soll wiederum mit graphischen Visualisierungen unterstützt werden. Damit die unterschiedlichen Streuungen gut ersichtlich sind, werden die Abweichungen der absoluten Häufigkeiten vom Erwartungswert visualisiert, da dies um den Wert 0 herum streut (Biehler und Prömmel 2013, 23). Als Beispiel kann hier wieder der fünfzigfache beziehungsweise zweihundertfache Münzwurf herangezogen werden, welche in Abb. 3.5 visualisiert sind.

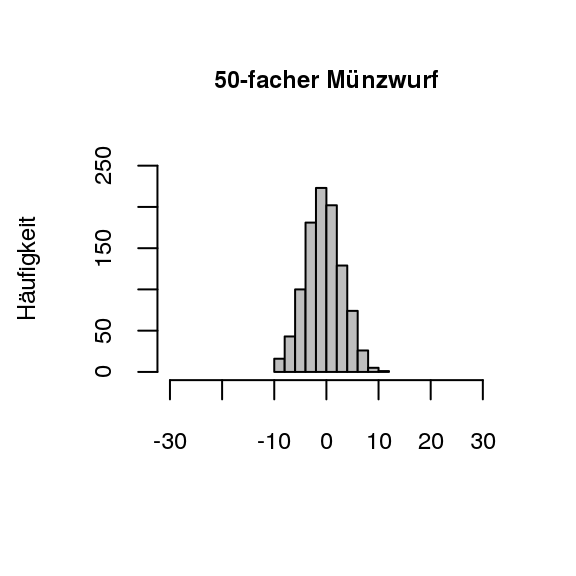
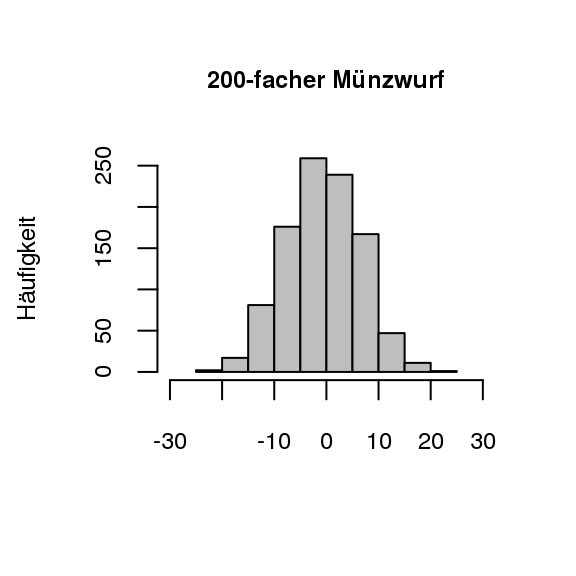
Figure 3.5: Münzwürfe im Vergleich (1000 Versuchswiederholungen)

In den beiden Grafiken in Abb. 3.5 ist gut ersichtlich, dass die absoluten Häufigkeiten beim zweihundertfachen Münzwurf mehr streuen als beim fünfzigfachen Münzwurf. Dabei ist anzumerken, dass sich die Verhältnisse bei den Streuungen im Vergleich umgekehrt haben (Biehler und Prömmel 2013, 23). Mit diesen Überlegungen lässt sich das Streuungsverhalten der absoluten und relativen Häufigkeiten im Hinblick auf den Stichprobenumfang auch wie folgt zusammenfassen:

\(\text{ }\)	50-facher Münzwurf	200-facher Münzwurf
absolute Häufigkeiten - \(\mathbb{E}W\)	geringe Streuung	große Streuung
relative Häufigkeiten - \(\mathbb{E}W\)	große Streuung	geringe Streuung

[absolute Häufigkeit und Erwartungswert]Wie bereits beschrieben, wurden die beiden Histogramme erstellt, indem die Abweichungen der absoluten Häufigkeiten für das Ereignis “Kopf” vom jeweiligen Erwartungswert (\(n/2\)) berechnet wurden. Wenn beispielsweise in der 50er-Münzserie die absolute Häufigkeit für “Kopf” 27 beträgt, dann ist die Abweichung vom Erwartungswert 2. Dieses Experiment wird \(1000\)-mal wiederholt und ergibt dann die Häufigkeitsverteilung der Abweichungen um \(\mathbb{E}X_{50}=25\). Analog wird das Histogramm für die 200er-Münzserie erstellt (Biehler und Prömmel 2013, 23). Durch das Darstellen der absoluten Häufigkeiten im Zusammenhang mit dem Erwartungswert \((n/2)\) wird unter anderem die Fehlvorstellung des “Gambler’s Fallacy” angesprochen. Dabei bedeutet “Gambler’s Fallacy”, dass sich Abweichungen der relativen Häufigkeiten zum Erwartungswert selbst korrigieren beziehungsweise ausgleichen (Schnell 2014, 14:35+45).

3.5 \(\frac{1}{\sqrt{n}}\)-Gesetz theoretisch und Verbindung zu \(\sigma\)-Regeln

[Ausgangssituation]In der letzten Stufe wurde die Frage, auf welche Art die Streubreite vom Stichprobenumfang \(n\) abhängt, empirisch (durch das Ausprobieren an verschiedenen Beispielen) behandelt. In dieser Stufe sollen die mathematischen Konzepte im Hintergrund herausgearbeitet und das \(1/\sqrt{n}\)-Gesetz theoretisch betrachtet werden. Diese theoretische Betrachtung kann in der Oberstufe nach der Binomialverteilung und der Modellierung des Münzwurfes als Bernoulli-Kette thematisiert werden. Aus den Modellierungen lässt sich dann das \(1/\sqrt{n}\)-Gesetz herleiten (Biehler und Prömmel 2013, 23).

[Prognoseintervall]Im Gegensatz zu den Konfidenzintervallen, welche den Schluss von Stichproben auf die Grundgesamtheit erlauben, machen Prognoseintervalle den umgekehrten Schluss. Das heißt, sie thematisieren die Frage, welche Aussagen sich über Stichproben bei bekannter Grundgesamtheit machen lassen, wenn man die Binomialverteilung durch die Normalverteilung approximiert (Meyer 2013, 10). Eine Sicherheitswahrscheinlichkeit \(\alpha\) wird vorgegeben und dazu \(k \in \mathbb{R}\) bestimmt, sodass \[\begin{align*} \alpha = \int_{-k}^{k} \Phi(x)dx \end{align*}\] gilt, wobei \(\Phi(x)\) die standardisierte Normalverteilung ist. Wenn die Grundgesamtheit binomialverteilt ist, mit Erfolgswahrscheinlichkeit \(p\) und absoluter Häufigkeit \(H\) für Erfolg in einer \(n\)-elementigen Stichprobe, dann gilt mit Wahrscheinlichkeit \(\alpha\) \[\begin{align*} |H-\mu| &\leq k \cdot \sigma\\ \text{und}\\ |H-n \cdot p| &\leq k \cdot \sqrt{n \cdot p \cdot (1-p)} \end{align*}\] Durch Division durch \(n\) erhält man die relative Häufigkeit \[\begin{align*} h = \frac{H}{n} \end{align*}\] für Erfolg. Die Grenzen des Prognoseintervalls bestimmen sich dann durch \[\begin{align*}p \pm k \cdot \frac{\sqrt{n\cdot p \cdot (1-p)}}{n}=p \pm k \cdot \frac{\sqrt{p \cdot (1-p)}}{\sqrt{n}}. \end{align*}\] (vgl. Meyer (2013), S. 10) In Intervallschreibweise wäre dies dann \[\begin{align*} h \in [p \pm k \cdot \frac{\sqrt{p \cdot (1-p)}}{\sqrt{n}}]. \end{align*}\] [\(\sigma\)-Regeln]Die Idee hinter den \(\sigma\)-Regeln ist die Abweichung vom Erwartungswert \(\mu\) mit der Standardabweichung \(\sigma\) als Einheit zu berechnen. Aus \(P_{\mu, \sigma}([\mu\pm k \cdot \sigma])\) für \(k \in \mathbb{N}\) folgt mit dem Transformationssatz: \[\begin{align*} &P_{\mu, \sigma}([\mu - k \cdot \sigma, \mu + k \cdot \sigma])\\ &= \Phi \left( \frac{\mu + k\sigma - \mu}{\sigma} \right) - \Phi \left( \frac{\mu - k\sigma - \mu}{\sigma} \right)\\ &= \Phi(k)-\Phi(-k)=\Phi(k)-(1-\Phi(k)) = 2 \Phi(k)-1. \end{align*}\]

Mit der Tabelle der Standardnormalverteilung \(\Phi\) können diese Werte berechnet werden. Bei einer normalverteilten Größe mit Erwartungswert \(\mu\) und Standardabweichung \(\sigma\) gilt:

• circa \(68\%\) der Werte liegen im Intervall \([\mu \pm \sigma]\)
• circa \(95\%\) der Werte liegen im Intervall \([\mu \pm 2\sigma]\)
• circa \(99\%\) der Werte liegen im Intervall \([\mu \pm 3\sigma]\)

Betrachtet man eine normalverteilte Zufallsvariable \(X\), kann man diese Regeln noch weiter ergänzen:

• \(\mathbb{P}(\mu - 1,64 \leq X \leq \mu + 1,64) \approx 0,90\)
• \(\mathbb{P}(\mu - 1,96 \leq X \leq \mu + 1,96) \approx 0,95\)
• \(\mathbb{P}(\mu - 2,58 \leq X \leq \mu + 2,58) \approx 0,99\)

Diese Faustregeln sind auch unter dem Namen “\(\sigma\)-Regeln” bekannt.(vgl. Büchter und Henn 2005, 292; Kütting und Sauer 2014, 318f; Bartz 2018, 2)

[\(\frac{1}{\sqrt{n}}\)-Gesetz]Mit diesen Vorüberlegungen kann nun das \(\frac{1}{\sqrt{n}}\)-Gesetz mathematisch gefasst werden. Wie in den Stufen davor wird wieder der Münzwurf thematisiert. Dazu soll \(X\) eine binomialverteilte Zufallsvariable sein, welche angibt, wie oft die Münze auf “Kopf” fällt. Da die relative Häufigkeit im Vordergrund unserer Überlegung steht, soll dies die Zufallsvariabel \(Y\) mit \(Y = X/n\) modellieren. Die Standardabweichung einer binomialverteilten Zufallsvariablen ist \(\sqrt{n \cdot p \cdot (1-p)}\), somit: \[\begin{align*} \sigma(X)&=\sqrt{n \cdot p \cdot (1-p)}\\ \text{und}\\ \sigma(Y)&=\frac{\sqrt{n \cdot p \cdot (1-p)}}{n} = \frac{\sqrt{p \cdot (1-p)}}{\sqrt{n}} \end{align*}\] Durch die Normalapproximation der Binomialverteilung, den Vorüberlegungen zu Prognoseintervallen und den \(\sigma\)-Regeln erhält man: \[\begin{align*} \mathbb{P}(X \in [np - 1,96\sigma(X), np + 1,96\sigma(X)]) \approx 95\% \end{align*}\] Die Streubreite beträgt also \(2 \cdot 1,96 \sqrt{n \cdot p \cdot (1-p)}\). Im Intervall [0;1] kann man \(p \cdot (1-p)\) mit \(1/4\) abschätzen. Somit: \[\begin{align*} 2 \cdot 1,96 \sqrt{n \cdot p \cdot (1-p)} \leq 2 \cdot 1,96 \sqrt{n \cdot \frac{1}{4}} \leq 2 \sqrt{n} \end{align*}\] Aus der Modellierung der Zufallsvariablen Y durch \(Y=\frac{X}{n}\) folgt: \[\begin{align*} \mathbb{P}(Y \in [p-1,96\sigma(Y), p + 1,69\sigma(Y)]) \approx 95 \% \end{align*}\] Im Vergleich zum \(95\%\)-Bereich der Zufallsvariablen \(X\) hat sich der Erwartungswert \(\mu\) von \(np\) auf \(p\) geändert, da die Zufallsvariable die relative Häufigkeit (dividiert durch \(n\)) wiedergibt. Nun kann noch \(\sigma(Y)\) eingesetzt werden: \[\begin{align*} \mathbb{P} \left( Y \in \left[ p - 1,96 \frac{\sqrt{p(1-p)}}{\sqrt{n}}, p + 1,96 \frac{\sqrt{p(1-p)}}{\sqrt{n}} \right] \right) \approx 95\% \end{align*}\] Aufgrund der Abschätzung von \(p(1-p) \leq \frac{1}{4}\) im Intervall \([0;1]\) folgt die Faustregel: \[\begin{align*} \mathbb{P} \left( Y \in \left[ p - \frac{1}{\sqrt{n}}, p + \frac{1}{\sqrt{n}} \right] \right) \approx 95 \% \end{align*}\]

Aus dieser Faustformel folgt das \(\frac{1}{\sqrt{n}}\)-Gesetz (Biehler und Prömmel 2013, 23).

3.6 Schritt zu Konfidenzintervallen

[Erweiterung]Das Stufenkonzept von Biehler und Prömmel (2013) sieht keine Behandlung der Konfidenzintervalle vor. Riemer (1991) merkt jedoch an, dass auf einem elementaren Niveau eine Vorstellung zu Konfidenzintervallen erarbeitet werden kann. Da jedoch die Konfidenzintervalle ein Teil des Phänomenkomplexes des empirischen Gesetzes der großen Zahlen sind, fließen diese in die Erweiterung ein (Prömmel 2013, 67).

[Hintergrund]Bis jetzt war der Erwartungswert \(\mu\) beziehungsweise die Wahrscheinlichkeit \(p\) bekannt. In den meisten interessanten oder praktischen Fällen sind \(\mu\) und \(p\) jedoch unbekannt (Prömmel 2013, 74). Mithilfe von Konfidenzintervallen berechnet man Bereiche (vgl. Bereichsschätzung), welche sich mit \(\mu\) und \(p\) gut überdecken. Konfidenzintervalle beschreiben einen (meist symmetrischen) Bereich um einen festgelegten Wert. Vereinfacht lässt sich sagen, dass sich jedes Konfidenzintervall auf die Form \[\begin{align*} \text{Schätzer } \pm \text{ Sicherheitsparameter } \cdot \text{ Standardfehler} \end{align*}\]

zurückführen lässt (Janczyk und Pfister 2013, 65–66).

[Berechnung der Intervalle]Es seien \(X_1, X_2, \dots X_n\) stochastisch unabhängige Zufallsvariablen mit dem Erwartungswert \(\mu\) und der Varianz \(\sigma^2\). Sowohl \(\mu\) als auch \(p\) sind unbekannt. Dann kann man folgendermaßen zu einem Konfidenzintervall mit Konfidenzniveau \(\alpha\) kommen. Dabei muss \(z\) so gewählt werden, dass \[\begin{align*} \alpha = 2 \Phi(z) -1 \end{align*}\] gilt. Dann erhält man durch Umformung \(z_\alpha\) \[\begin{align*} 2 \cdot \Phi(z) &= \alpha +1 \\ \Phi(z) &= \frac{\alpha+1}{2}\\ z_\alpha &= \Phi^{-1}\left(\frac{\alpha+1}{2}\right) \end{align*}\] Dies kann nun für das Konfidenzintervall verwendet werden, es ergibt sich: \[\begin{align*} \left[\bar{x} - z_\alpha \cdot \frac{\sigma}{\sqrt{n}}, \bar{x} + z_\alpha \cdot \frac{\sigma}{\sqrt{n}}\right] \end{align*}\] Falls die Standardabweichung \(\sigma\) unbekannt ist, dann kann \(\sigma\) durch \[\begin{align*} s_n = \sqrt{\frac{1}{n-1}\sum_{i=1}^n(x_i - \bar{x})^2} \end{align*}\] geschätzt werden. Bei einem kleinen Stichprobenumfang \(n\) kann \(z_\alpha\) durch die Testgröße \(t_\alpha\) der Student-t-Verteilung ausgedrückt werden. Bei binomialverteilten Zufallsvariablen, welche die Laplace-Bedingung erfüllen, kann auch die Approximationsformel \[\begin{align*} \left[h-z_\alpha \cdot \frac{\sqrt{h \cdot (1-h)}}{\sqrt{n}}, h+z_\alpha \cdot \frac{\sqrt{h \cdot (1-h)}}{\sqrt{n}}\right] \end{align*}\]

verwendet werden (Prömmel 2013, 74).

[Zusammenhang mit Prognoseintervallen]Zwischen den Konfidenzintervallen und den Prognoseintervallen gibt es einen starken Zusammenhang. Mit einem \(\alpha \cdot 100\%\)-Prognoseintervall kann von einem relativen Anteil \(p\) der Grundgesamtheit auf die relative Häufigkeit \(h\) in der Stichprobe geschlossen werden. Andererseits ist es auch möglich, basierend auf einem \(\alpha \cdot 100\%\)-Konfidenzintervall eine “Hochrechnung” von der beobachteten relativen Häufigkeit \(h\) in der Stichprobe auf unbekannten Anteil \(p\) in der Grundgesamtheit zu schließen (Prömmel 2013, 75).

[Einflussfaktoren]Für die Breite des Konfidenzintervalls gibt es drei wesentliche Faktoren. Einerseits nimmt der Sicherheitsparameter Einfluss auf das Konfidenzintervall. Eine höhere Sicherheit (\(99\%\) statt \(95\%\)) führt beispielsweise zu einem breiteren Konfidenzintervall. Wenn eine geringere Varianz der Grundgesamtheit angenommen wird, weist in der Regel die Stichprobe auch eine geringere Varianz auf, was zu einer Verkleinerung des Intervalls führt. Ein größerer Stichprobenumfang führt zur Verkleinerung des Konfidenzintervalls, da in der Regel eine Verkleinerung des Standardfehlers vorherrscht (Janczyk und Pfister 2013, 67).

[Interpretation]Die Frage, die noch offen bleibt, ist: “Was genau bedeutet ein Konfidenzintervall?” Eine weiterverbreitete Interpretation bezieht sich auf die Wahrscheinlichkeit, mit welcher der geschätzte Populationsparameter im Konfidenzintervall liegt. Das heißt, dass ein Populationsparameter also zu \(95\%\)-iger Wahrscheinlichkeit im berechneten \(95\%\) Konfidenzintervall liegen soll. Jedoch sollte dabei nicht vergessen werden, dass die Konfidenz von \(95\%\) keine Eigenschaft des Populationsparameters, sondern des Schätzverfahrens ist. In Abb. 3.6 wird diese Interpretation anhand eines Beispiels veranschaulicht. Das Beispiel beruht auf einer normalverteilten Variablen mit dem Erwartungswert \(\mu = 2{,}3\) und einer Standardabweichung \(\sigma = 0{,}1\). Es wurden 50 unabhängige Stichproben mit \(n = 100\) gezogen und jeweils das \(95\%\) Konfidenzintervall berechnet. In Abb. 3.6 ist jedoch zu sehen, dass nicht jedes Konfidenzintervall \(\mu\) (eingezeichnete Linie) beinhaltet.

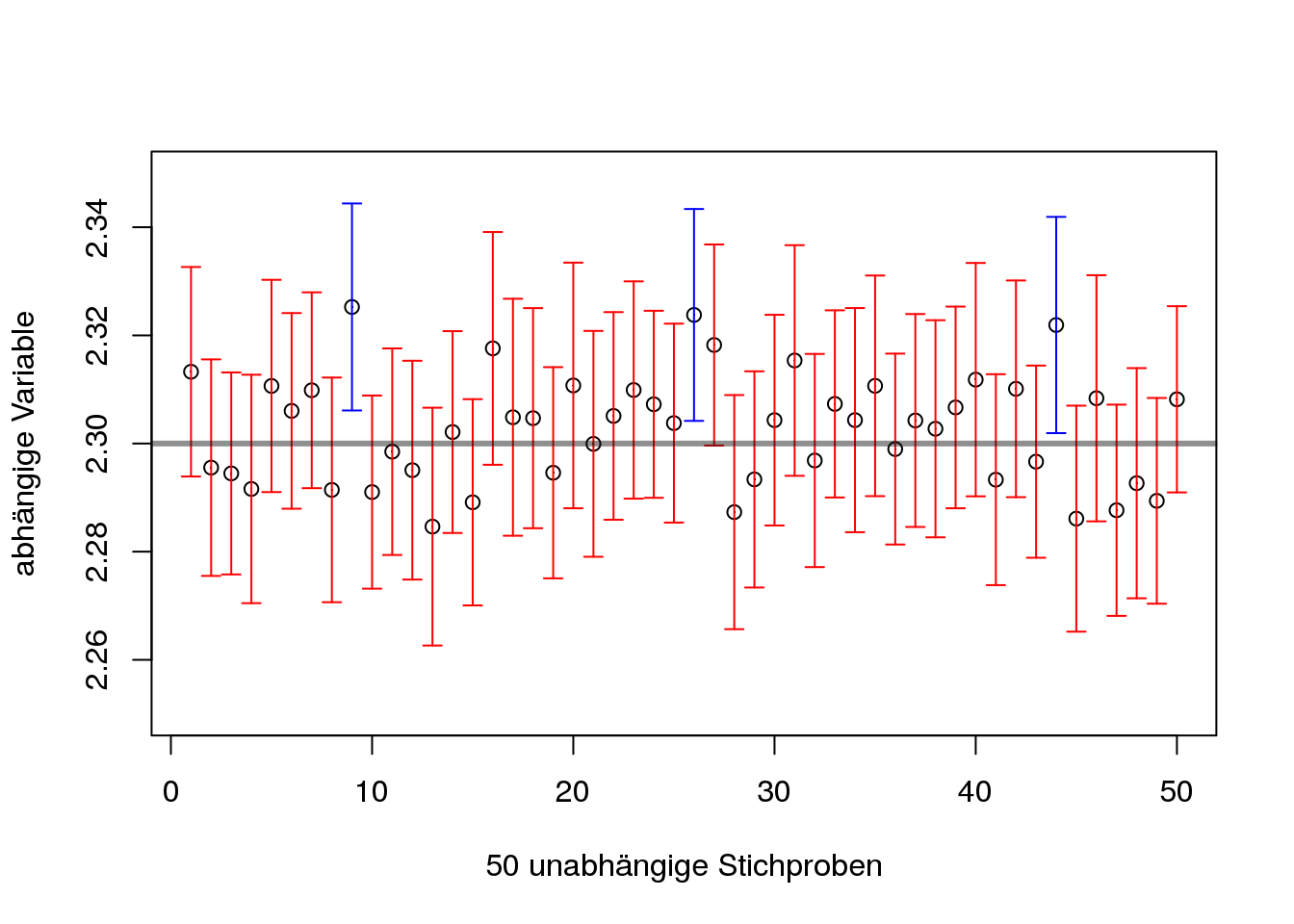
Figure 3.6: Vergleich von Konfidenzintervallen

3.7 Zusammenfassung der Vorstellungen und Erkenntnisse

[Stufenmodell als Experiment]Im Stufenmodell von Biehler und Prömmel (2013) werden einige wichtige Basiselemente der Stochastik behandelt. Ein Vorteil der Simulation, welche das Stufenmodell begleiten sollte, ist, dass es durch variierende und dynamische Repräsentationen die Zufallsexperimente greifbar macht, ohne dass eine reale und zeitintensive Durchführung des Experiments benötigt wird. Zusätzlich können die Ergebnisse mithilfe theoretischer Zugänge gestützt und überprüft werden (Biehler und Prömmel 2013, 18).

[Stabilisierung bei häufiger Durchführung]Der Zufall ist immer mit Muster und Variabilität verbunden. Muster ergeben sich auf lange Sicht eines Zufallsexperiments. Bei kurzer Sicht hingegen sind die Ergebnisse zufälliger Vorgänge mit Variabilität durchdrungen. Bei vielen Menschen ist jedoch fälschlicherweise das Gesetz der kleinen Zahlen fest verankert. Es muss deutlich gesagt werden, dass das Gesetz der kleinen Zahlen kein Gesetz ist, welches in der Mathematik vorkommt, sondern nur der Name für eine Fehlvorstellung. Jedoch sollte gerade durch das Stufenmodell die Vorstellung des empirischen Gesetzes der großen Zahlen mit der Musterbildung im Zufall verbunden werden. Denn erst nach häufiger Durchführung des Zufallsexperiments stabilisieren sich die relativen Häufigkeiten um einen bestimmten Wert. Das empirische Gesetz der großen Zahlen hat den Namen Gesetz bekommen, da es bei der Interpretation des starken Gesetzes der großen Zahlen Sinn macht (vgl. Schnell 2014; Biehler und Prömmel 2013).

[Vorhersage der relativen Häufigkeit]Zwar stabilisieren sich die relativen Häufigkeiten bei häufiger Durchführung eines Zufallsexperiments um einen bestimmten Wert, jedoch ist es nicht möglich diesen mit Sicherheit vorherzusagen. Wenn beispielsweise eine Münze zwanzig Mal geworfen wird, sind für die relativen Häufigkeiten alle Brüche \(0/20, 1/20, \dots , 20/20\) möglich. Aus diesem Grund kann man nur sicher aussagen, dass die relative Häufigkeit zwischen 0 und 1 liegt (vgl. Biehler und Prömmel 2013).

[keine Stabilisierung der absoluten Häufigkeit]Für die relativen Häufigkeiten ist die Stabilisierung bekannt, jedoch gibt es kein Gesetz der großen Zahlen für die absoluten Häufigkeiten. Es wäre eine grobe Fehlvorstellung, wenn eine Stabilisierung der absoluten Häufigkeiten um \(n/2\) angenommen wird (vgl. Biehler und Prömmel 2013).